Virtual Lab

About Us

Department of Electronics and Communication Engineering, Vivekananda College of Engineering and Technology, Puttur

Electronics and Communication Engineering is a 4-year degree programme, affiliated to the VTU was started in the year 2001. ECE is the utilization of science and math applied to practical problems in the field of communications. It includes designing, fabrication, testing, maintenance, supervision, and manufacturing of electronic equipments in entertainment, media, hospitals (Medical Electronics), computer control systems, broadcast, communication systems and in defence. It also engage in research, design, development and testing of electronic equipment used in various communication systems. The defined courses aim to prepare students to play a leading role in the continuing adventure of modern communication, research, designing, building and marketing the next generation of products.

Convolution

Example for Linear Convolution

∞

∑ x(k)h(n-k)=y(n)

k=-∞

Eg: let x(n)={1,2,3} and h(n)={1,1,1}

y(0)=∑x(k)h(-k)=x(0)h(0)=1
y(1)=∑x(k)h(1-k)=x(0)h(1)+x(1)h(0)=3
y(2)=∑x(k)h(2-k)=x(0)h(2)+x(1)h(1)+x(2)h(0)=6
y(3)=∑x(k)h(3-k)=x(1)h(2)+x(2)h(1)=5
y(4)=∑x(k)h(4-k)=x(2)h(0)=3

Example for Circular Convolution

N-1

∑ x(k)h((n-k))_N=y(n)

k=0

Eg: let x(n)={1,2,3} and h(n)={1,1,1}

y(0)=∑x(k)h((-k))₃=x(0)h(0)+x(1)h((-1))₃+x(2)h((-2))₃=6
y(1)=∑x(k)h((1-k))₃=x(0)h(1)+x(1)h((0))₃+x(2)h((-1))₃=6
y(2)=∑x(k)h((2-k))₃=x(0)h(2)+x(1)h((1))₃+x(2)h((0))₃=6

Correlation

Equation with Example

∞

∑ x(k)h(k-n)=y(n)

k=-∞

Eg: let x(n)={1,2,3} and h(n)={3,2,1}

y(0)=∑x(k)h(k)=x(0)h(0)+x(1)h(1)+x(2)h(2)=10
y(1)=∑x(k)h(k-1)=x(1)h(0)+x(2)h(1)=12
y(2)=∑x(k)h(k-2)=x(2)h(0)=9
y(-1)=∑x(k)h(k+1)=x(0)h(1)+x(1)h(2)=8
y(-2)=∑x(k)h(k+2)=x(0)h(2)=1

FFT

Equation with Example

N-1

∑ x(n)e^-j2Πkn/N=X(k)

n=0

Eg: let x(n)={1,2,3,4}

X(0)= x(0)e⁰+x(1)e⁰+x(2)e⁰+x(3)e⁰=10
X(1)= x(0)e⁰+x(1)e^-j2Π/4+x(2)e^-j4Π/4+x(3)e^-j6Π/4=-2+2j
X(2)= x(0)e⁰+x(1)e^-j4Π/4+x(2)e^-j8Π/4+x(3)e^-j12Π/4=-2
X(3)= x(0)e⁰+x(1)e^-j6Π/4+x(2)e^-j12Π/4+x(3)e^-j18Π/4=-2-2j

Fourier Transform of Rectangular Pulse

Equation with Example. Click here for better image quality.

Fourier Transform of Sinc Pulse

Equation with Example. Click here for better image quality.

DCT

Equation with Example

N-1

∑ x(n)cos(Π(2n+1)k/2N)*w(k)=X(k)

n=0

With w(0)=sqrt(1/N) and w(k)=sqrt(2/N), for k=1,2..N-1

Eg: let x(n)={1,2,3}

X(0)= (x(0)cos(0)+x(1)cos(0)+x(2))*sqrt(1/3)=3.464
X(1)= (x(0)cos(Π/6)+x(1)cos(3Π/6)+x(2)cos(5Π/6))*sqrt(2/3)=-1.414
X(2)= (x(0)cos(2Π/6)+x(1)cos(6Π/6)+x(2)cos(10Π/6))*sqrt(2/3)=0

DWT

DWT process

MFCC

Inputs

Select wav file for Feature extraction

Enter the Frame size(Window size) Example:512

Enter the Percentage of overlap in frame size Example:0.5

Enter the No.of filter banks Example:20

MFCC algorithm usage guidelines

1. Provide .wav file only.
2. wav sample files are available for download here.
3. These algorithm returns Original speech signal and MFCC features.
4. The dimension of MFCC features depends on filter bank size, provided by the user.
5. Data furnished by these algorithm may used in Speech recognization system for validation

FIR Filter

Inputs

Enter the order Example:21

Enter the cut of frequency Example:0.785

Enter the function window Example:hamm/hann

Low pass FIR filter analysis

h_d(n)= 1/2 _-wc∫^wc e^-jwαe^jwndw

h_d(n)= sin(wc(n-α))/(Π(n-α))

h(n)= h_d(n)w(n), 0<=n<=N-1

H(w)= ∑h(n)e^-jwn

Difference Equation

Inputs

Enter first numerator coefficeients Example:1 2

Enter first denominator coefficeients Example:1 -4 3

Enter the input sequence Example:1 2 3 4

Difference equation

y(n)= - ∑_k=0^N a_ky(n-k)+∑_k=0^M b_kx(n-k)

Eg: let x(n)={1,2,3,4}, b0=1,b1=2, a1=-4,a2=3
y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)+b1x(n-1)+b2x(n-2)
y(0)=4y(-1)-3y(-2)+x(0)+2x(-1)=1
y(1)=4y(0)-3y(-1)+x(1)+2x(0)=8
y(2)=4y(1)-3y(0)+x(2)+2x(1)=36
y(3)=4y(2)-3y(1)+x(3)+2x(2)=130

IIR filter

Inputs

Enter the passband frequency in Hz Example:1500

Enter the stopband frequency in Hz Example:3000

Enter the passband attenuation in dB Example:3

Enter the stopband attenuation in dB Example:10

Enter the sampling frequency in Hz Example:8000

Design procedure

Eg: Let Fp=1500Hz, Fs=3000Hz, ap=3dB, as=10dB, Fsamp=8000Hz, T=1/Fsamp ωp=2πFp/Fsamp=0.375π, ωs=2πFs/Fsamp=0.75π Ωp=(2/T)tan(ωp/2)=1.069x10⁴,Ωs=(2/T)tan(ωs/2)=3.862x10⁴

Obtain order N= log(10^{(ap/10) -1}/10^{(as/10) -1})/(2log(Ωp/Ωs)~=1

Obtain ωc=ωp=0.375π

Obtain H_an(s) = 1/(s+1)

Obtain H_Lp(s) = H_an(s)|s->s/Ωp= (1.069x10⁴)/(s+1.069x10⁴)

Obtain H(z)=H_Lp(s)|z->(2/T)(1-z^-1)/(1+z^-1)=(0.4006+0.4006z^-1)/(1-0.1977z^-1)

Obtain H(w)= H(z)|z->e^jw

Sampling Theorem

Inputs

Enter signal frequency (fm) in Hz Example:10

Enter sampling frequency (fs) in Hz Example:100

Enter the resolution of analog signal x(t) Example:0.0001

Sampling theorem statement and cases

Sampling theorem statement : A signal x(t) can be reconstructed successfully from its samples x(n) if fs>=2fm
Three cases of sampling theorem

Case(i) Oversampling: fs>>2fm, reconstruction is possible, but not effective since it consumes more memory

Case(ii)Nyquist rate sampling: fs=2fm,reconstruction is possible, effective since it does not consume more memory

Case(iii)Under sampling: fs<<2fm,reconstruction is not possible

Overlap Save method

Inputs

Enter the long length input sequence x(n) Example:1 -1 1 2 -1 0 1 2 1

Enter the filter coefficients h(n) Example:1 -1 1

Enter the value of N block size Example:5

Overlap save algorithm

Given the values of x(n), h(n) and length of block size N.
Overlap save method uses following steps to obtain the response y(n).
Step 1: Padd L-1 zeros to h(n) to make its length N. Where N=L+M-1 and M is length of h(n)
Step 2: Decompose x(n) into x1(n), x2(n), x3(n) and so on. To obtain x1(n), we padd (M-1) zeros at the beginning and extract first L samples of x(n). Similarly x2(n) is obtained by considering the last (M-1) samples of x1(n) and next L samples of x(n). These process is repeated untill we visit all samples of x(n).
Step 3: Find the circular convolution between x1(n) and h(n), indicate it by y1(n)
Step 4: Repeat step 3 to obtain y2(n), y3(n) and so on.
Step 5: Discard the first (M-1) samples of each output sequences, remaining samples are fitted one after another to get the final sequence.

Overlap add method

Inputs

Enter the long length input sequence x(n) Example:1 -1 1 2 -1 0 1 2 1

Enter the filter coefficients h(n) Example:1 -1 1

Enter the value of N block size Example:5

Overlap add algorithm

Given the values of x(n), h(n) and length of block size N.
Overlap save method uses following steps to obtain the response y(n).
Step 1: Padd L-1 zeros to h(n) to make its length N. Where N=L+M-1 and M is length of h(n)
Step 2: Decompose x(n) into x1(n), x2(n), x3(n) and so on. To obtain x1(n), we extract first L samples of x(n) and padd (M-1) zeros at the end. Similarly x2(n) is obtained by considering the next L samples of x(n) and padding (M-1) zeros at the end. These process is repeated untill we visit all samples of x(n).
Step 3: Find the circular convolution between x1(n) and h(n), indicate it by y1(n)
Step 4: Repeat step 3 to obtain y2(n), y3(n) and so on.
Step 5: Add the last (M-1) samples of each output sequences with the first (M-1) samples of succeedding output sequences, remaining samples are fitted one after another to get the final sequence.

Radix-2 DIT FFT

Inputs

Enter the 8 point sequence Example:1 1 1 1 0 0 0 0

Radix-2 DIT FFT Algorithm for N=8

In Radix-2 DIT FFT algorithm, the input sequence x(n) is decimated in time domain. The decimation process is repeated untill x(n) becomes a 2 point sequence. Radix-2 is a process in which N point DFT's are represented using several two point DFT's.

Inverse Radix-2 DIT FFT

Inputs

Enter the 8 point real DFT sequence Example:4 1 0 1 0 1 0 1

Enter the 8 point imag DFT sequence Example:0 -2.41421 0 -0.41421 0 0.41421 0 2.41421

Inverse Radix-2 DIT FFT Algorithm for N=8

In Inverse Radix-2 DIT FFT algorithm, the output sequence x(n) is decimated in time domain. The decimation process is repeated untill x(n) becomes a 2 point sequence. Radix-2 is a process in which N point IDFT's are represented using several two point IDFT's.

Radix-2 DIF FFT

Inputs

Enter the 8 point sequence Example:1 1 1 1 0 0 0 0

Radix-2 DIF FFT algorithm

In Radix-2 DIF FFT algorithm, the input sequence x(n) is taken in natural order. The output sequence X(k) is taken in bit-reversed order. Radix-2 is a process in which N point DFT's are represented using several two point DFT's.

ASK Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency Example:100

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Amplitude Shift Keying theory

1. In ASK, the amplitude of the carrier signal is varied in accordance with the message signal
2. Carrier is transmitted if message bit is 1, is blocked if message bit is 0.
3. Also known as ON-OFF keying

FSK Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency for bit-1 Example:50

Enter the carrier frequency for bit-0 Example:20

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Frequency Shift Keying theory

1. In FSK, the frequency of the carrier signal is varied in accordance with the message signal
2. In FSK two carrier frequency are to be selected for bi1-1 and bit-0 respectively
3. Carrier frequency Fc1 is transmitted if message bit is 1.
4. Carrier frequecny Fc2 is transmitted if message bit is 0.

PSK Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency Example:20

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Phase Shift Keying theory

1. In PSK, the phase of the carrier signal is varied in accordance with the message signal
2. Carrier with no phase-shift is transmitted if message bit is 1.
3. Carrier with 180 degree phase-shift is transmitted if message bit is 0.

DPSK Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency Example:20

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Enter the initial bit for encoding Example:1/0

Differential Phase Shift Keying theory

1. In DPSK, the phase of the carrier signal is varied in accordance with the message signal
2. The message signal is differentially encoded(EXNOR) using initial bit d as 1 or 0.
3. Carrier with no phase-shift is transmitted if message bit is 1.
4. Carrier with 180 degree phase-shift is transmitted if message bit is 0.

QPSK Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency Example:20

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Quadrature Phase Shift Keying theory

1. In QPSK, the phase of the carrier signal is varied in accordance with the message signal
2. Here instead of single bit, di-bits are considered for modulation.
3. If message bit is 00, Carrier with 135 degree phase-shift is transmitted.
4. If message bit is 10, Carrier with 45 degree phase-shift is transmitted.
5. If message bit is 11, Carrier with 315 degree phase-shift is transmitted.
6. If message bit is 01, Carrier with 225 degree phase-shift is transmitted.

QAM Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency Example:20

Enter the bit duration Example:0.1

Enter the simulation time Example:1

Quadrature Amplitude Modulation

1. In QAM, the amplitude and phase of the carrier signal is varied in accordance with the message signal
2. Here instead of single bit, four(quad)bits are considered for modulation.
3. Using quad bits, we get 16 possible combination with varied amplitude and phase.

TDM Modulation

Inputs

Enter the sampling frequency Example:1000

Enter the carrier frequency-1 Example:5

Enter the carrier frequency-2 Example:20

Enter the control signal bit duration Example:0.01

Enter the simulation time Example:1

TDM Modulation

1. In TDM, two or more signals are multiplexed in time based on the control signal.
2. If number of message signals to be multiplexed is restricted to two and control signal is high, first message signal is transmitted.
3. If control signal is low, second message signal is transmitted.

Find-S

Inputs

Select csv file to determine Maximally Specific Hypothesis

Find-S Algorithm usage guidelines

1. Provide .csv file only.
2. Last column of the CSV file should have Yes or No labels.
3. CSV sample files are available for download here.

Decision Tree-ID3

Inputs

Select csv file to determine Learned Decision tree

ID3 Algorithm usage guidelines

1. Provide .csv file only.
2. Last column of the CSV file should have Yes or No labels.
3. CSV sample files are available for download here.

Candidate-Elimination Algorithm

Inputs

Select csv file to determine Generic and Specific Boundary

Candidate-Elimination Algorithm usage guidelines

1. Provide .csv file only.
2. Last column of the CSV file should have Yes or No labels.
3. CSV sample files are available for download here.

Logistic Regression

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Logistic Regression Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. CSV sample files are available for download here.

KNN Classifier

Inputs

Select csv file for Classification

Enter K Neigbors Example:5

Enter the test dataset size Example:0.25

KNN Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. Number of neighors should be entered.
5. CSV sample files are available for download here.

Random Forest

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Random Forest Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. Max depth parameter for Classifier is set to 2.
5. CSV sample files are available for download here.

Linear Discriminant Classifier

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Linear Discriminant Analysis(LDA) Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. No. of components for classifier is to default= min(no of features,no of classes-1).
5. CSV sample files are available for download here.

Decision Tree

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Decision Tree Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. Max depth parameter for Classifier is set to 2.
5. CSV sample files are available for download here.

Linear Support Vector Machine

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Linear SVM Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. Linear Kernel is selected.
5. CSV sample files are available for download here.

Non Linear Support Vector Machine

Inputs

Select csv file for Classification

Enter the test dataset size Example:0.25

Non Linear SVM Classifier usage guidelines

1. Provide .csv file only.
2. Remove column and row names from the csv file if existing.
3. Last column of the CSV file should have class label in integer form.
4. RBF Kernel is selected.
5. CSV sample files are available for download here.

Circuits Lab

Full Window

Circuits Lab Videos

Op-Amp Inverting Amplifier

Half Adder

Half Wave Rectifier

Block Diagram Reduction

Inputs

Enter numerator coefficeients of first subystem Example:4

Enter denominator coefficeients of first subsystem Example:1 2 1

Enter numerator coefficeients of second subystem Example:1

Enter denominator coefficeients of second subsystem Example:1 2

Block diagram reduction details

Pole-Zero PLot

Inputs

Enter numerator coefficeients Example:4

Enter denominator coefficeients Example:1 2 1

Pole-Zero Plot

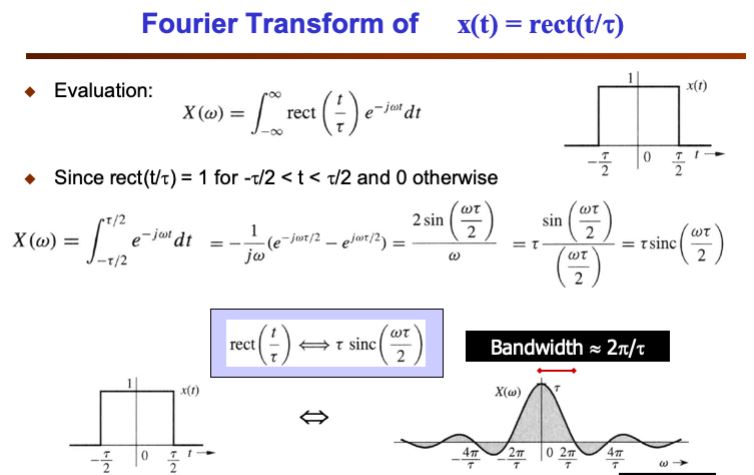
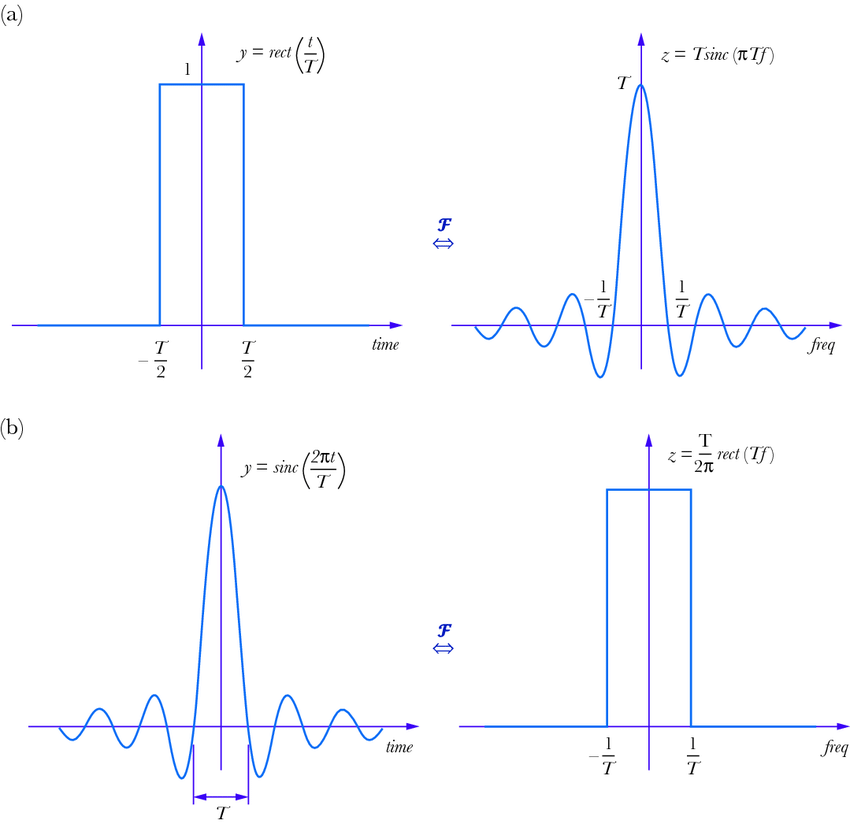
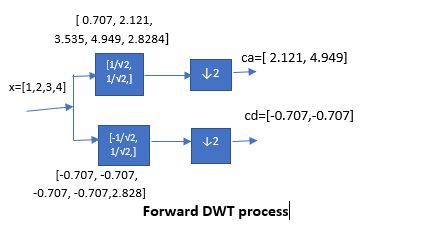
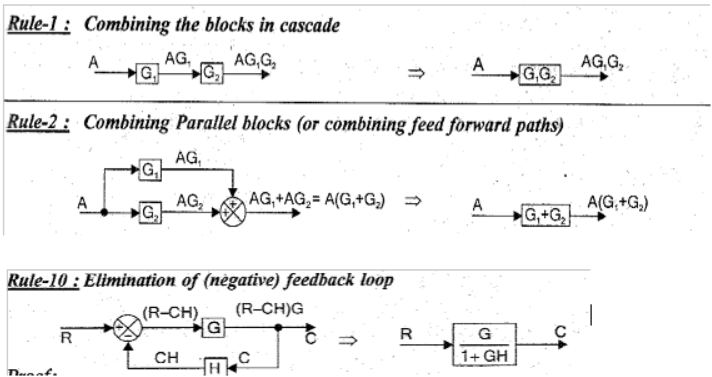
Zeros: Zeros of a transfer function are the values of H(s) for which the transfer function becomes zero. Geometrically, zeros represent points in the complex plane where the transfer function intersects the x-axis (real axis).Zeros can influence the system's response by affecting the locations of peaks, dips, or cancellations in the frequency response.

Poles: Poles of a transfer function are the values of H(s) for which the transfer function becomes infinite or undefined. Geometrically, poles represent points in the complex plane where the transfer function diverges or approaches infinity. Poles are crucial in determining the stability and transient response of a system. The stability of a system is directly related to the location of its poles: if all the poles are in the left half of the complex plane, the system is stable.

Second order underdamped system for varying damping ratio

Inputs

Select 4 different damping ratio's(0 to 1) Example:0.1 0.4 0.6 0.8

Time response of second order system

Frequency response of Second order system

Inputs

Enter natural frequency(ω_n) Example:1

Enter damping factor(ζ) Example:1

Frequency response of second order system

Transfer function of second order system with natural frequency ω_n and damping coefficient ζ is given by

H(s)=(ω_n²)⁄(s²+2ζω_ns + ω_n²)

Routh Array stability analysis

Inputs

Enter the coeffcients of characteristic equation(ω_n) Example:1 1 3 1 6

Stability analysis using Routh criterion

The Routh-Hurwitz criterion is a mathematical test used in control systems and signal processing to determine the stability of a linear time-invariant (LTI) system. Specifically, it provides a way to determine whether all the roots of a given polynomial lie in the left half of the complex plane, which corresponds to a stable system

Contact

Department of Electronics and Comunication Engineering, Vivekananda College of Engineering and Technology Puttur

Location:

Neharunagara, Puttur, D. K. Karnataka

Email:

hod.ece@vcetputtur.ac.in

Call:+91 9743703473

Virtual Laboratory

Key Features:

About Us

Convolution

Correlation

FFT

Fourier Transform of Rectangular Pulse

Fourier Transform of Sinc Pulse

DCT

DWT

MFCC

FIR Filter

Difference Equation

IIR filter

Sampling Theorem

Overlap Save method

Overlap add method

Radix-2 DIT FFT

Inverse Radix-2 DIT FFT

Radix-2 DIF FFT

ASK Modulation

FSK Modulation

PSK Modulation

DPSK Modulation

QPSK Modulation

QAM Modulation

TDM Modulation

Find-S

Decision Tree-ID3

Candidate-Elimination Algorithm

Logistic Regression

KNN Classifier

Random Forest

Linear Discriminant Classifier

Decision Tree

Linear Support Vector Machine

Non Linear Support Vector Machine

Circuits Lab

Circuits Lab Videos

Block Diagram Reduction

Pole-Zero PLot

Second order underdamped system for varying damping ratio

Frequency response of Second order system

Routh Array stability analysis

Contact

Location:

Email:

Call:+91 9743703473